排序
连续型分布
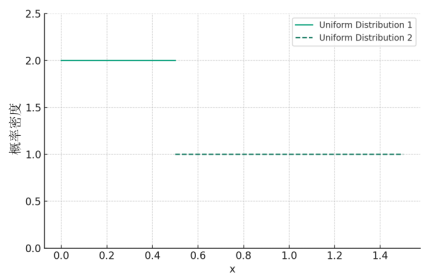
概率密度函数 对于连续型随机变量,由于其取值不能一一列举出来,因而不能用离散型随机变量的分布列来描述其取值的概率分布情况。但人们在大量的社会实践中发现连续型随机变量落在任一区间([a,b...
Python:魔法函数
Python 的魔法函数,又称为特殊方法,是 Python 类中定义的一组特殊的方法,具有一些独特的特性和用途。这些方法以双下划线(__)开头和结尾,它们在 Python 编程中扮演着特殊角色。魔法函数不...
Python:生成器
在Python中,生成器是一种用于创建迭代器的简单而强大的工具。它们允许程序员编写能够记住执行状态的函数,并在需要时产生一个值,而不是一次性返回所有值。 什么是生成器? 生成器是一个返回迭...
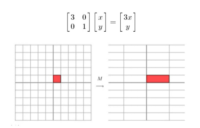
向量与矩阵
向量的正交 两两正交的非零向量组成的向量组称为正交向量组,若\(a_{1},a_{2},\cdots,a_{r}\) 是两两正交的非零向量,则\(a_{1},a_{2},\cdots,a_{r}\) 线性无关。例如:己知三维空间\(R^{3}\) ...
Python:函数的局部和全局变量
在Python中,理解局部变量和全局变量是关键的,因为它们决定了变量的可见性和作用域。这对于编写结构良好且易于维护的代码至关重要。 全局变量 定义:全局变量在函数外部定义,并且在整个程序中...
Python:语法糖
在编程世界中,有一个词语听起来既甜蜜又神秘:语法糖(Syntactic Sugar)。这个术语并不是指真正的糖,而是指那些让程序员的生活变得更加甜美的编程语言特性。在Python中,语法糖无处不在,它...
向量乘法
向量的点积和内积 记录:没有对2、3、N维向量的各种乘法计算的情况进行更细致的划分和讲解,如叉积只展示了两个三维向量的叉积计算。 向量的点积和内积(Inner Product, dot product),用\(\cd...
经验概率分布
先来具体看一下经验分布函数的定义:首先,根据大数定理(详见1.4.1节),在抽样的次数足够大时,可以把抽样结果的频率当做概率。所以经验分布函数的核心思想就是把频率分布函数当作概率分布函...
Python:多态
Python中的多态是面向对象编程中的一个重要概念。多态性(Polymorphism)指的是能够使用统一的接口来操作不同类型的对象。在Python中,多态表现为不同类的对象对同一消息可以作出不同的响应。以...