数学基础共27篇
数学基础模块涵盖了高等数学、概率论等与AI密切相关的基础知识，为学习者打下扎实的数学基础。通过深入浅出的讲解，帮助你理解线性代数、微积分、概率统计等数学概念在人工智能中的应用。无论是模型训练、数据分析，还是算法优化，掌握这些核心数学原理将为深入学习AI技术提供强有力的支撑。
排序
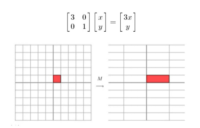
向量与矩阵
向量的正交 两两正交的非零向量组成的向量组称为正交向量组，若\(a_{1},a_{2},\cdots,a_{r}\) 是两两正交的非零向量，则\(a_{1},a_{2},\cdots,a_{r}\) 线性无关。例如：己知三维空间\(R^{3}\) ...
10个月前
微分与函数的单调性、极值和凹凸性
函数单调性 函数单调性定义：若\(fx)\)在\((a,b)\)内可导，如果\(f'(x)>0\)，那么函数在\((a,b)\)内单调递增；如果\(f'(x)<0\)，那么函数在\((a.b)\)内单调递减。 用微分的定义（微分解释了...
10个月前
概率论基础
概率论介绍 概率论主要研究随机事件。人们对某些事件发生的可能性高低一般都有直观的认识，所以未经特殊训练就会使用“可能”、“不可能”之类的词汇。概率论会介绍如何量化这种可能性。 为了更...
10个月前
偏微分与全微分
在机器学习中，许多函数都是多变量的。需要知道每个输入变量的变化如何影响输出。偏微分正是用于这个目的的。例如，在线性回归中可能要最小化多变量函数（即损失函数）。偏微分指明每个权重的变...
10个月前
梯度与方向导数
梯度是机器学习中的核心概念，尤其是在优化中，梯度提供了一个方向，指明如何调整参数以最小化损失函数。在梯度下降算法中，使用梯度的负方向来更新模型的权重，以逐步减少误差。 梯度是一个向...
10个月前
泰勒公式与麦克劳林公式
泰勒公式\(P_n(x)\) 泰勒公式允许用多项式来近似复杂的函数，这在算法中有时用于简化计算。例如，在高斯过程回归和一些其他贝叶斯方法中，泰勒展开用于线性化关于后验的计算。 泰勒公式的本质是...
10个月前
重识积分
积分的几何解释是：该函数曲线下的面积。 积分的物理解释是： 积分的物理意义随不同物理量而不同，比如对力在时间上积分就是某段时间内力的冲量；如果是对力在空间上的积分就是某段位移里力做的...
10个月前不定积分和反导数
不定积分在机器学习中主要用于计算函数的原函数，尤其是在概率密度函数和累积分布函数之间的转换中。例如，在概率论和统计中，累积分布函数 (CDF) 是概率密度函数 (PDF) 的不定积分。对于某些模...
10个月前
定积分与牛顿-莱布尼茨公式
牛顿-莱布尼茨公式提供了一种计算定积分的方法，即通过求取两个不定积分的差值。在机器学习中，这常常用于计算概率或期望值。例如在贝叶斯机器学习中，经常需要计算概率分布的期望值或方差。使...
10个月前
微积分的基本定理
微积分不仅研究一个函数更深刻的性质（即更精细的乘除法），还研究不同函数之间的关系。举一个圆的例子，如果已知圆的周长，怎么求面积？ 积分近似求解圆面积 上图中，当知道周长求面积时就用到...
10个月前
