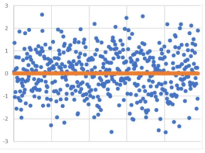
相关性分析 在函数关系（FunctionalRelationship)中，一个变量完全由另一个变量决定。例如，给定一个方程\(y=2x+3\) ，对于每一个\(x\) 的值， \(y\) 只有一个确定的值。这种关系可以是线性的、...

Python作为一种编程语言，其设计哲学强调的是代码的可读性和简洁性。其中，推导式（comprehensions）是Python提供的一种非常有用且独特的特性。它们允许程序员用一种简洁而直观的方式来创建数据...

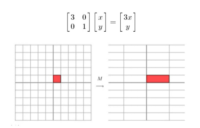
什么是向量 在上述讲解中，已经涉及了三个主要的数学系统：线性方程组、函数图形和矩阵。现在将介绍第四个系统：向量。线性代数的一个核心挑战是它涵盖了多个数学系统。要成功掌握线性代数，关...

线性方程组与矩阵 先从线性方程组开始讲起，线性方程组的一般形式如下所示： $$\left\{\begin{aligned}a_{11}x_1+a_{12}x_2+&\cdots +a_{1n}x_n=b_1\\a_{21}x_2+a_{22}x_2+&\cdots +a_{...

统计推断是依据从总体中抽取的一个简单随机样本对总体进行分析和判断。统计推断的基本问题可以分为两大类：一类是参数估计问题，一类是假设检验问题。本节主要讨论总体参数的点估计和区间估计。...

Python的上下文管理器是一种高级特性，允许程序员进行有效的资源管理和异常处理。这个概念在处理文件、网络连接和其他需要显式释放的资源时特别有用。 什么是上下文管理器？ 上下文管理器是实现...

Python中的继承是面向对象编程（OOP）的一个基本特性，它允许一个类（称为子类）继承另一个类（称为父类或基类）的属性和方法。这里是关于Python继承的一些关键点： 基本概念 父类（基类）：父...

迭代器在Python中是一种基本但却经常被忽视的概念。它们是Python处理集合数据的基石，无论是简单的列表还是复杂的自定义数据结构。理解迭代器的工作原理对于深入理解Python及其数据处理能力至关...

向量的正交 两两正交的非零向量组成的向量组称为正交向量组，若\(a_{1},a_{2},\cdots,a_{r}\) 是两两正交的非零向量，则\(a_{1},a_{2},\cdots,a_{r}\) 线性无关。例如：己知三维空间\(R^{3}\) ...

在机器学习中，许多函数都是多变量的。需要知道每个输入变量的变化如何影响输出。偏微分正是用于这个目的的。例如，在线性回归中可能要最小化多变量函数（即损失函数）。偏微分指明每个权重的变...