排序
微积分的基本定理
微积分不仅研究一个函数更深刻的性质(即更精细的乘除法),还研究不同函数之间的关系。举一个圆的例子,如果已知圆的周长,怎么求面积? 积分近似求解圆面积 上图中,当知道周长求面积时就用到...
偏微分与全微分
在机器学习中,许多函数都是多变量的。需要知道每个输入变量的变化如何影响输出。偏微分正是用于这个目的的。例如,在线性回归中可能要最小化多变量函数(即损失函数)。偏微分指明每个权重的变...
Python:六大数据类型理论与示例
在这篇文章中,我们深入探讨了Python中的六大基本数据类型:数字(Number)、字符串(String)、列表(List)、元组(Tuple)、集合(Set)、字典(Dictionary)。每种数据类型都有其特定用途和...
图神经网络基础:图论
引言 图在我们身边随处可见;现实世界中的物体通常是以它们与其它事物的联系来定义的。一组物体以及它们之间的联系,都可以自然地表达为一个图。十多年来,研究人员已经开发了在图数据上操作的...
泰勒公式与麦克劳林公式
泰勒公式\(P_n(x)\) 泰勒公式允许用多项式来近似复杂的函数,这在算法中有时用于简化计算。例如,在高斯过程回归和一些其他贝叶斯方法中,泰勒展开用于线性化关于后验的计算。 泰勒公式的本质是...
经验概率分布
先来具体看一下经验分布函数的定义:首先,根据大数定理(详见1.4.1节),在抽样的次数足够大时,可以把抽样结果的频率当做概率。所以经验分布函数的核心思想就是把频率分布函数当作概率分布函...
Python:模块,包,库
Python是一种广泛使用的高级编程语言,其强大之处部分源于其模块化的设计。理解模块、包和库之间的区别和联系对于有效地使用Python至关重要。 模块(Module) 模块是Python编程中最基本的组织单...
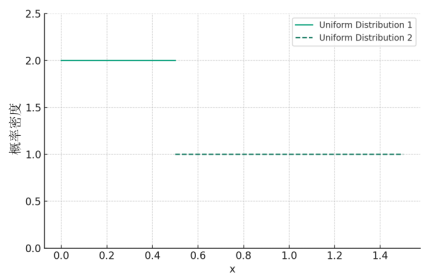
连续型分布
概率密度函数 对于连续型随机变量,由于其取值不能一一列举出来,因而不能用离散型随机变量的分布列来描述其取值的概率分布情况。但人们在大量的社会实践中发现连续型随机变量落在任一区间([a,b...
Python: for,while循环语句
While循环 while循环用于在给定条件为真时重复执行一段代码。它会一直执行循环体内的代码,直到条件不再为真。这种循环特别适合于你不知道需要执行循环多少次的情况,只要条件满足,循环就会继...
重拾微分
微分(differential)和导数(derivative)都与函数的变化率有关,它们是两个相关但不完全相同的概念。首先一起深入了解这两者的定义和区别。 导数 导数描述了一个函数在某一点上的切线斜率。如...