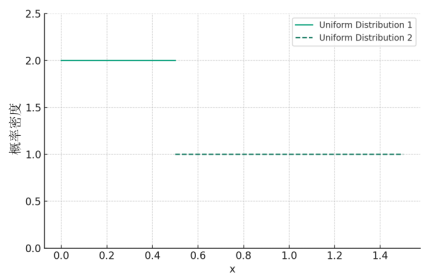
概率密度函数 对于连续型随机变量，由于其取值不能一一列举出来，因而不能用离散型随机变量的分布列来描述其取值的概率分布情况。但人们在大量的社会实践中发现连续型随机变量落在任一区间([a,b...

1.两点分布 如果随机变量(X) 的分布列如下： $$\begin{array}{l}P{X=1}=p\bigl(0<p<1\bigr)\\P{X=0}=q=1-p\end{array}$$ 则称(X) 服从两点分布。两点分布也叫伯努利分布（Bermoulli）或0-...

拉格朗日乘子法简介 函数\(y=f(x)\)在平面直角坐标系中的图像是一条曲线 函数\(z=f(x,y)\)在空间直角坐标系中的图像是一个曲面 那么如何表示一个在空间直角坐标系中的图像是空间曲线的函数呢 这...

相关性分析 在函数关系（FunctionalRelationship)中，一个变量完全由另一个变量决定。例如，给定一个方程\(y=2x+3\) ，对于每一个\(x\) 的值， \(y\) 只有一个确定的值。这种关系可以是线性的、...

微分（differential）和导数（derivative）都与函数的变化率有关，它们是两个相关但不完全相同的概念。首先一起深入了解这两者的定义和区别。 导数 导数描述了一个函数在某一点上的切线斜率。如...

在机器学习中，尤其是在深度学习和神经网络中，链式法则用于计算复合函数的导数，这在反向传播算法中尤为关键。具体来说，当训练一个深度神经网络时，需要计算损失函数相对于每个权重的梯度。由...

统计推断是依据从总体中抽取的一个简单随机样本对总体进行分析和判断。统计推断的基本问题可以分为两大类：一类是参数估计问题，一类是假设检验问题。本节主要讨论总体参数的点估计和区间估计。...

函数单调性 函数单调性定义：若\(fx)\)在\((a,b)\)内可导，如果\(f'(x)>0\)，那么函数在\((a,b)\)内单调递增；如果\(f'(x)<0\)，那么函数在\((a.b)\)内单调递减。 用微分的定义（微分解释了...

概率论介绍 概率论主要研究随机事件。人们对某些事件发生的可能性高低一般都有直观的认识，所以未经特殊训练就会使用“可能”、“不可能”之类的词汇。概率论会介绍如何量化这种可能性。 为了更...

叉乘（普通乘法） 矩阵乘法（Matmul Product）是两个矩形相乘的操作，其结果是另一个矩阵。定义如下： 设有两个矩阵\(\boldsymbol{A}\)和\(\boldsymbol{b}\)，令\(\boldsymbol{A}\)是一个\(m\ti...