最新发布第9页
排序
微积分的基本定理
微积分不仅研究一个函数更深刻的性质(即更精细的乘除法),还研究不同函数之间的关系。举一个圆的例子,如果已知圆的周长,怎么求面积? 积分近似求解圆面积 上图中,当知道周长求面积时就用到...
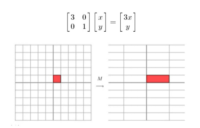
向量与矩阵
向量的正交 两两正交的非零向量组成的向量组称为正交向量组,若\(a_{1},a_{2},\cdots,a_{r}\) 是两两正交的非零向量,则\(a_{1},a_{2},\cdots,a_{r}\) 线性无关。例如:己知三维空间\(R^{3}\) ...
Python:if条件判断语句
比较运算符和关系运算符: 本文将介绍Python中常见的比较运算符,如 ==(等于)、!= 和 <>(不等于)、>(大于)、<(小于)、>=(大于或等于)和 <=(小于或等于)。 它还介...
经验概率分布
先来具体看一下经验分布函数的定义:首先,根据大数定理(详见1.4.1节),在抽样的次数足够大时,可以把抽样结果的频率当做概率。所以经验分布函数的核心思想就是把频率分布函数当作概率分布函...
多项式回归算法
算法解读 多项式回归是回归分析的一种形式,它允许因变量 \(y\) 与自变量 \(x\) 之间的关系模型化为 \(x\) 的 \(n\) 次多项式。多项式回归的标准形式如下:$$y=\beta_0+\beta_1 x+\beta_2 x^2+\b...
Python:继承
Python中的继承是面向对象编程(OOP)的一个基本特性,它允许一个类(称为子类)继承另一个类(称为父类或基类)的属性和方法。这里是关于Python继承的一些关键点: 基本概念 父类(基类):父...
文章类型分类项目
项目背景 在数据科学和机器学习的领域中,文本分析一直是一个引人注目的话题。这个项目的核心挑战是利用机器学习技术,根据文章或书籍的概要预测其类型。这不仅是一个技术挑战,涉及到复杂的文...
Swin Transformer:窗口化的Transformer
0.引言 Swin Transformer是2021年微软研究院发表在ICCV(International Conference on Computer Vision)上的一篇文章,并且已经获得ICCV 2021最佳论文(Best Paper)的荣誉称号。Swin Transfor...
VAN:基于卷积实现的注意力
0.引言 虽然Transformer最初是为自然语言处理任务而设计的,但最近已经在各种计算机视觉领域掀起了风暴。然而,图像是有空间信息的二维数据,这给计算机视觉中应用Transformer带来了三个挑战: ...