排序
偏微分与全微分
在机器学习中,许多函数都是多变量的。需要知道每个输入变量的变化如何影响输出。偏微分正是用于这个目的的。例如,在线性回归中可能要最小化多变量函数(即损失函数)。偏微分指明每个权重的变...
梯度与方向导数
梯度是机器学习中的核心概念,尤其是在优化中,梯度提供了一个方向,指明如何调整参数以最小化损失函数。在梯度下降算法中,使用梯度的负方向来更新模型的权重,以逐步减少误差。 梯度是一个向...
泰勒公式与麦克劳林公式
泰勒公式\(P_n(x)\) 泰勒公式允许用多项式来近似复杂的函数,这在算法中有时用于简化计算。例如,在高斯过程回归和一些其他贝叶斯方法中,泰勒展开用于线性化关于后验的计算。 泰勒公式的本质是...
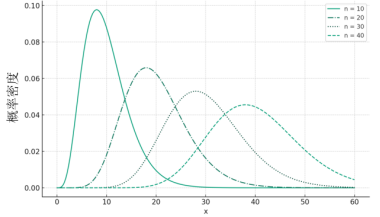
统计量和抽样分布
统计量 在数理统计学中,把研究对象的全体所构成的集合称为总体或母体,而把组成总体的每一个元素称为个体。在实际中,总体的分布往往不可得,因此统计学基本可以看作是用样本来推测总体分布情...
相关性分析
相关性分析 在函数关系(FunctionalRelationship)中,一个变量完全由另一个变量决定。例如,给定一个方程\(y=2x+3\) ,对于每一个\(x\) 的值, \(y\) 只有一个确定的值。这种关系可以是线性的、...
线性方程组
线性方程组与矩阵 先从线性方程组开始讲起,线性方程组的一般形式如下所示: $$\left\{\begin{aligned}a_{11}x_1+a_{12}x_2+&\cdots +a_{1n}x_n=b_1\\a_{21}x_2+a_{22}x_2+&\cdots +a_{...
重拾微分
微分(differential)和导数(derivative)都与函数的变化率有关,它们是两个相关但不完全相同的概念。首先一起深入了解这两者的定义和区别。 导数 导数描述了一个函数在某一点上的切线斜率。如...
微分的链式法则
在机器学习中,尤其是在深度学习和神经网络中,链式法则用于计算复合函数的导数,这在反向传播算法中尤为关键。具体来说,当训练一个深度神经网络时,需要计算损失函数相对于每个权重的梯度。由...