数学基础 第3页
数学基础模块涵盖了高等数学、概率论等与AI密切相关的基础知识，为学习者打下扎实的数学基础。通过深入浅出的讲解，帮助你理解线性代数、微积分、概率统计等数学概念在人工智能中的应用。无论是模型训练、数据分析，还是算法优化，掌握这些核心数学原理将为深入学习AI技术提供强有力的支撑。
排序
假设检验
假设检验的目的与参数估计的目的相同，都是根据样本求总体的参数，但是思想正好相反。可以把参数估计看作正推，即根据样本推测总体：而假设检验是反证，即先在总体上作某项假设，用从总体中随机...
7个月前梯度与方向导数
梯度是机器学习中的核心概念，尤其是在优化中，梯度提供了一个方向，指明如何调整参数以最小化损失函数。在梯度下降算法中，使用梯度的负方向来更新模型的权重，以逐步减少误差。 梯度是一个向...
7个月前
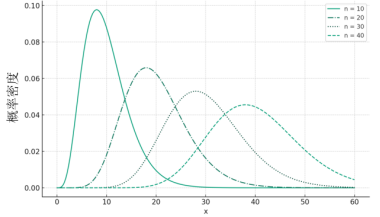
统计量和抽样分布
统计量 在数理统计学中，把研究对象的全体所构成的集合称为总体或母体，而把组成总体的每一个元素称为个体。在实际中，总体的分布往往不可得，因此统计学基本可以看作是用样本来推测总体分布情...
7个月前矩阵乘法
叉乘（普通乘法） 矩阵乘法（Matmul Product）是两个矩形相乘的操作，其结果是另一个矩阵。定义如下： 设有两个矩阵\(\boldsymbol{A}\)和\(\boldsymbol{b}\)，令\(\boldsymbol{A}\)是一个\(m\ti...
7个月前
微分的链式法则
在机器学习中，尤其是在深度学习和神经网络中，链式法则用于计算复合函数的导数，这在反向传播算法中尤为关键。具体来说，当训练一个深度神经网络时，需要计算损失函数相对于每个权重的梯度。由...
7个月前拉格朗日乘子法
拉格朗日乘子法简介 函数\(y=f(x)\)在平面直角坐标系中的图像是一条曲线 函数\(z=f(x,y)\)在空间直角坐标系中的图像是一个曲面 那么如何表示一个在空间直角坐标系中的图像是空间曲线的函数呢 这...
7个月前离散型分布
1.两点分布 如果随机变量(X) 的分布列如下： $$\begin{array}{l}P{X=1}=p\bigl(0<p<1\bigr)\\P{X=0}=q=1-p\end{array}$$ 则称(X) 服从两点分布。两点分布也叫伯努利分布（Bermoulli）或0-...
7个月前
