排序
向量的线性组合
什么是向量 在上述讲解中,已经涉及了三个主要的数学系统:线性方程组、函数图形和矩阵。现在将介绍第四个系统:向量。线性代数的一个核心挑战是它涵盖了多个数学系统。要成功掌握线性代数,关...
偏微分与全微分
在机器学习中,许多函数都是多变量的。需要知道每个输入变量的变化如何影响输出。偏微分正是用于这个目的的。例如,在线性回归中可能要最小化多变量函数(即损失函数)。偏微分指明每个权重的变...
向量空间与向量的线性相关和线性无关
向量空间指的是线性组合的集合,例如\(b\)的向量空间是整个二维空间: $$\boldsymbol{b}=x_{1}\begin{bmatrix}2\\1\\ \end{bmatrix}+x_{2}\begin{bmatrix}-1\\1\\ \end{bmatrix}$$ 即:在二维空...
相关性分析
相关性分析 在函数关系(FunctionalRelationship)中,一个变量完全由另一个变量决定。例如,给定一个方程\(y=2x+3\) ,对于每一个\(x\) 的值, \(y\) 只有一个确定的值。这种关系可以是线性的、...
梯度与方向导数
梯度是机器学习中的核心概念,尤其是在优化中,梯度提供了一个方向,指明如何调整参数以最小化损失函数。在梯度下降算法中,使用梯度的负方向来更新模型的权重,以逐步减少误差。 梯度是一个向...
向量乘法
向量的点积和内积 记录:没有对2、3、N维向量的各种乘法计算的情况进行更细致的划分和讲解,如叉积只展示了两个三维向量的叉积计算。 向量的点积和内积(Inner Product, dot product),用\(\cd...
泰勒公式与麦克劳林公式
泰勒公式\(P_n(x)\) 泰勒公式允许用多项式来近似复杂的函数,这在算法中有时用于简化计算。例如,在高斯过程回归和一些其他贝叶斯方法中,泰勒展开用于线性化关于后验的计算。 泰勒公式的本质是...
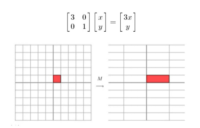
向量与矩阵
向量的正交 两两正交的非零向量组成的向量组称为正交向量组,若\(a_{1},a_{2},\cdots,a_{r}\) 是两两正交的非零向量,则\(a_{1},a_{2},\cdots,a_{r}\) 线性无关。例如:己知三维空间\(R^{3}\) ...
拉格朗日乘子法
拉格朗日乘子法简介 函数\(y=f(x)\)在平面直角坐标系中的图像是一条曲线 函数\(z=f(x,y)\)在空间直角坐标系中的图像是一个曲面 那么如何表示一个在空间直角坐标系中的图像是空间曲线的函数呢 这...