排序
Python:继承
Python中的继承是面向对象编程(OOP)的一个基本特性,它允许一个类(称为子类)继承另一个类(称为父类或基类)的属性和方法。这里是关于Python继承的一些关键点: 基本概念 父类(基类):父...
重拾微分
微分(differential)和导数(derivative)都与函数的变化率有关,它们是两个相关但不完全相同的概念。首先一起深入了解这两者的定义和区别。 导数 导数描述了一个函数在某一点上的切线斜率。如...
Python:迭代器
迭代器在Python中是一种基本但却经常被忽视的概念。它们是Python处理集合数据的基石,无论是简单的列表还是复杂的自定义数据结构。理解迭代器的工作原理对于深入理解Python及其数据处理能力至关...
矩阵乘法
叉乘(普通乘法) 矩阵乘法(Matmul Product)是两个矩形相乘的操作,其结果是另一个矩阵。定义如下: 设有两个矩阵\(\boldsymbol{A}\)和\(\boldsymbol{b}\),令\(\boldsymbol{A}\)是一个\(m\ti...
Python:类和对象
面向对象编程 VS 面向过程编程 在使用计算机语言进行代码编写时,常见的两种思路是面向对象编程和面向过程编程: (1)面向过程:根据业务逻辑从上到下写代码。(2)面向对象:将数据与函数绑定...
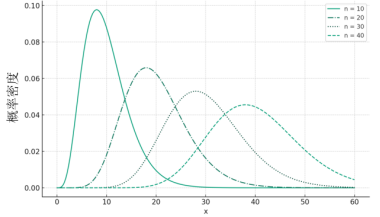
统计量和抽样分布
统计量 在数理统计学中,把研究对象的全体所构成的集合称为总体或母体,而把组成总体的每一个元素称为个体。在实际中,总体的分布往往不可得,因此统计学基本可以看作是用样本来推测总体分布情...
微分与函数的单调性、极值和凹凸性
函数单调性 函数单调性定义:若\(fx)\)在\((a,b)\)内可导,如果\(f'(x)>0\),那么函数在\((a,b)\)内单调递增;如果\(f'(x)<0\),那么函数在\((a.b)\)内单调递减。 用微分的定义(微分解释了...
Python:闭包
什么是闭包(Closure)? 在Python中,闭包是一个非常强大的概念。闭包,简而言之,是一个函数,它记住了其外部作用域中的变量,即使在该外部作用域已经执行完毕后。 闭包的构成 闭包通常涉及三...
向量的线性组合
什么是向量 在上述讲解中,已经涉及了三个主要的数学系统:线性方程组、函数图形和矩阵。现在将介绍第四个系统:向量。线性代数的一个核心挑战是它涵盖了多个数学系统。要成功掌握线性代数,关...