排序
图神经网络基础:图论
引言 图在我们身边随处可见;现实世界中的物体通常是以它们与其它事物的联系来定义的。一组物体以及它们之间的联系,都可以自然地表达为一个图。十多年来,研究人员已经开发了在图数据上操作的...
偏微分与全微分
在机器学习中,许多函数都是多变量的。需要知道每个输入变量的变化如何影响输出。偏微分正是用于这个目的的。例如,在线性回归中可能要最小化多变量函数(即损失函数)。偏微分指明每个权重的变...
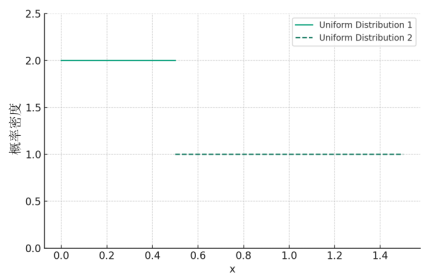
连续型分布
概率密度函数 对于连续型随机变量,由于其取值不能一一列举出来,因而不能用离散型随机变量的分布列来描述其取值的概率分布情况。但人们在大量的社会实践中发现连续型随机变量落在任一区间([a,b...
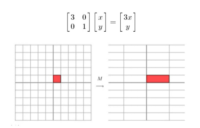
线性方程组
线性方程组与矩阵 先从线性方程组开始讲起,线性方程组的一般形式如下所示: $$\left\{\begin{aligned}a_{11}x_1+a_{12}x_2+&\cdots +a_{1n}x_n=b_1\\a_{21}x_2+a_{22}x_2+&\cdots +a_{...
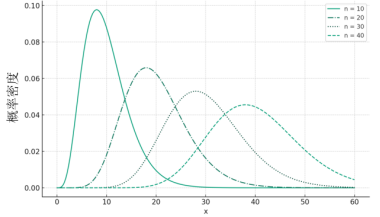
大数定律与中心极限定理
大数定律与中心极限定理是统计学家总结出的自然现象,是概率统计的基石。很多定理和推论都是基于它们之上的研究。 大数法则 讲个故事,一位数学家调查发现,欧洲各地男婴与女婴的出生比例是22:...
统计量和抽样分布
统计量 在数理统计学中,把研究对象的全体所构成的集合称为总体或母体,而把组成总体的每一个元素称为个体。在实际中,总体的分布往往不可得,因此统计学基本可以看作是用样本来推测总体分布情...
微积分的基本定理
微积分不仅研究一个函数更深刻的性质(即更精细的乘除法),还研究不同函数之间的关系。举一个圆的例子,如果已知圆的周长,怎么求面积? 积分近似求解圆面积 上图中,当知道周长求面积时就用到...
向量与矩阵
向量的正交 两两正交的非零向量组成的向量组称为正交向量组,若\(a_{1},a_{2},\cdots,a_{r}\) 是两两正交的非零向量,则\(a_{1},a_{2},\cdots,a_{r}\) 线性无关。例如:己知三维空间\(R^{3}\) ...
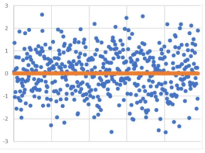
经验概率分布
先来具体看一下经验分布函数的定义:首先,根据大数定理(详见1.4.1节),在抽样的次数足够大时,可以把抽样结果的频率当做概率。所以经验分布函数的核心思想就是把频率分布函数当作概率分布函...